| Name | Comments on Applicability | Reference |
|---|
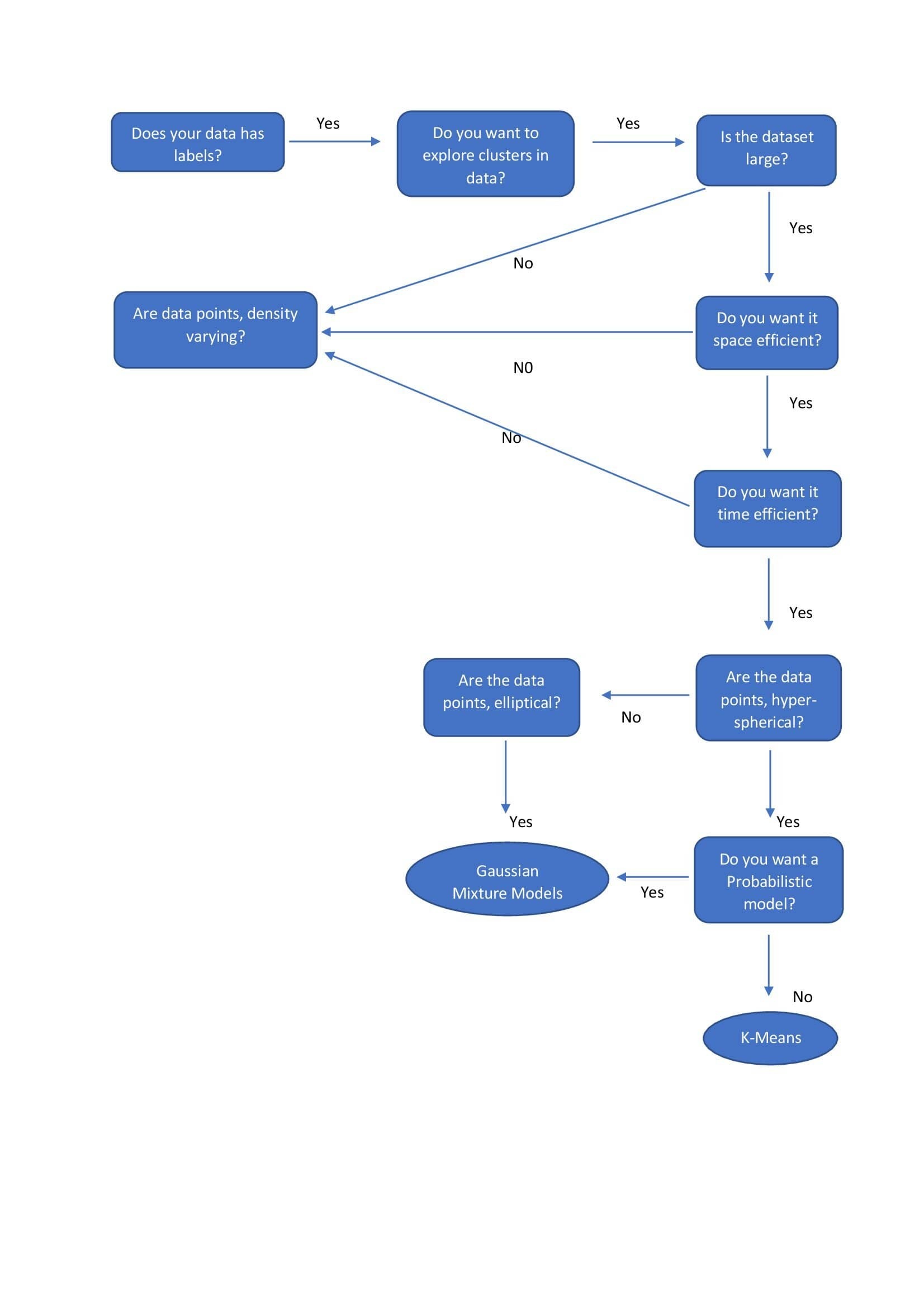
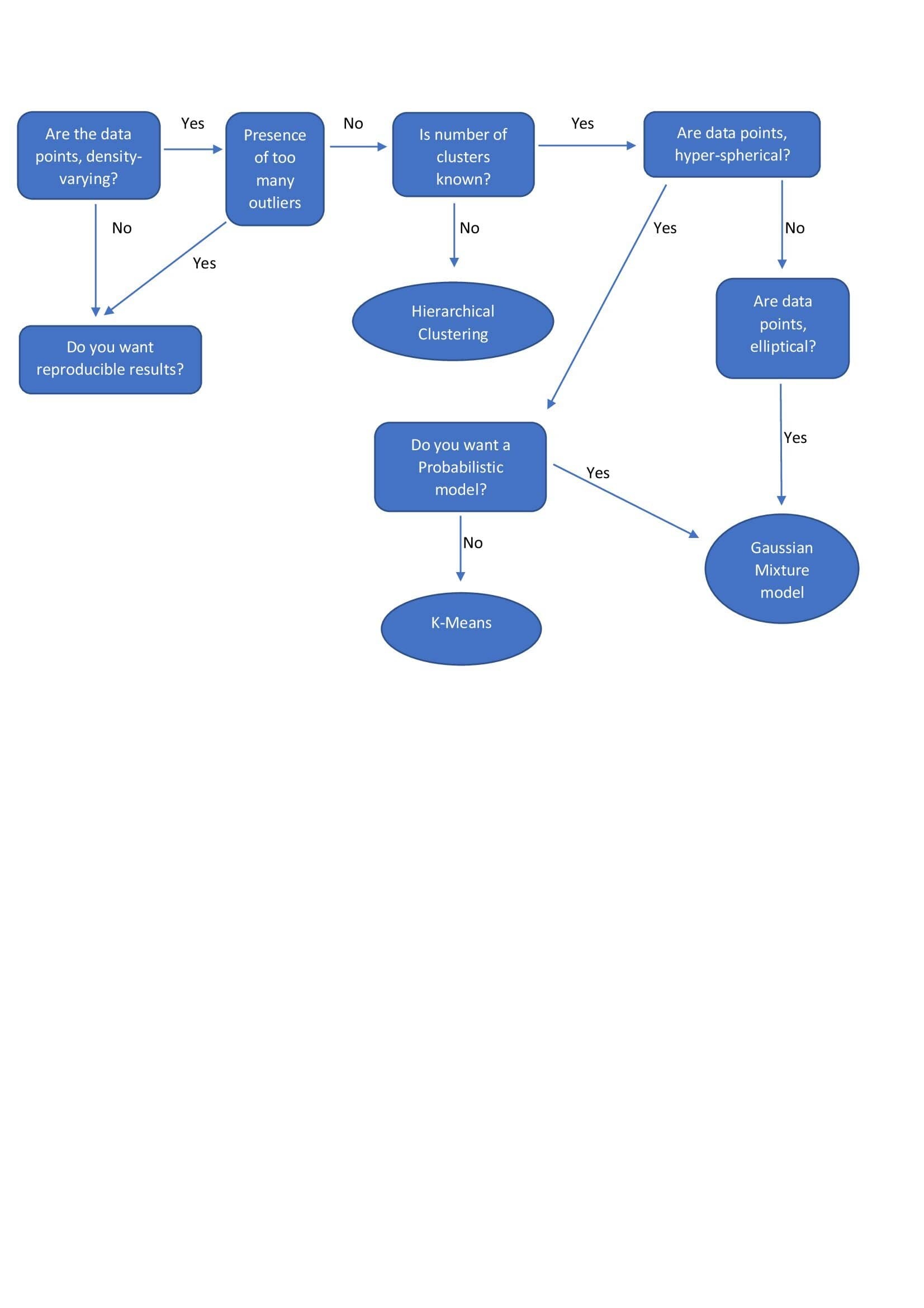
| Hierarchical Clustering | - (N-1) combination of clusters are formed to choose from.
- Expensive and slow. n×n distance matrix needs to be made.
- Cannot work on very large datasets.
- Results are reproducible.
- Does not work well with hyper-spherical clusters.
- Can provide insights into the way the data pts. are clustered.
- Can use various linkage methods(apart from centroid).
|
|
| k-means | - Pre-specified number of clusters.
- Less computationally intensive.
- Suited for large dataset.
- Point of start can be random which leads to a different result each time the algorithm runs.
- K-means needs circular data. Hyper-spherical clusters.
- K-Means simply divides data into mutually exclusive subsets without giving much insight into the process of division.
- K-Means uses median or mean to compute centroid for representing cluster.
|
|
| Gaussian Mixture Models | - Pre-specified number of clusters.
- GMs are somewhat more flexible and with a covariance matrix we can make the boundaries elliptical (as opposed to K-means which makes circular boundaries).
- Another thing is that GMs is a probabilistic algorithm. By assigning the probabilities to data points, we can express how strong is our belief that a given data point belongs to a specific cluster.
- GMs usually tend to be slower than K-Means because it takes more iterations to reach the convergence. (The problem with GMs is that they have converged quickly to a local minimum that is not very optimal for this dataset. To avoid this issue, GMs are usually initialized with K-Means.)
|
|
| DBSCAN | - No pre-specified no. of clusters.
- Computationally a little intensive.
- Cannot efficiently handle large datasets.
- Suitable for non-compact and mixed-up arbitrary shaped clusters.
- Uses density-based clustering. Cannot work well with density varying data points.
- Not effected by noise or outliers.
|
|